Mountain climbers and obsessive peak-baggers have a common goal: to stand atop a specific mountain or series of mountains. It is generally accepted that you must stand on the highest point of a mountain to claim a successful ascent. Thankfully, about 95% of the time, there is no dispute as to the mountain top’s exact location (true summit) and its exact elevation (true elevation). But about 5% of the time, things can get murky. Sometimes the location of the true summit is in dispute; sometimes the true elevation (measured in either in feet or meters, or both) is in dispute. This essay attempts to isolate and address these two issues.
Where is the true summit and how is it determined?
To answer this question, we must examine several generic cases (with specific illustrations of Idaho Mountains when possible). We shall start with the easiest case and then progressively handle more complicated cases.
CASE #1
The easiest case is one in which there is one, and only one, highest point. It may be a measured point using a USGS topo map’s figure or it may be the area above the highest contour line on the map (an unmeasured summit). In the latter case, there is only one “highest contour line.” But even in this simple case, you may have to wander around on a summit plateau searching for the “highest point” (measured or unmeasured). Sometimes, it’s just not possible to locate a clear, highest point on a particularly flat summit area. In other instances, some kind soul has built a cairn at what they consider to be the “highest point” and your search is probably unnecessary. In other cases, a surveyor has left a USGS benchmark, or rebar stuck in the ground, or a large cairn with a post in it to indicate exactly where the elusive high point is.
CASE #2
This is the case where a mountain has two measured summits of exactly the same height. THIS IS EXTREMELY UNUSUAL. In Idaho, Peak 8297 fits the bill. This peak is located just off US-93, south of Challis, at Broken Wagon Creek Road. The peak has a narrow summit ridge that stretches from South to North and is over a mile in length. The North Summit is measured at 8,297 feet. The South Summit is measured at 8,297 feet. Which one is the true summit? BOTH ARE. A true peak-bagger will climb both summits to claim this mountain. Doing only one isn’t enough. Why didn’t you climb the other one?
CASE #3
This is the most deceptive case. It is a case in which a measured summit appears to be the true summit, but isn’t. There is an unmeasured summit nearby that sits above a higher contour line than the measured summit. When climbing obscure mountain peaks in Idaho, this case occurs with a much greater frequency than you would think. If you simply look at the USGS topo map, you will be lured into believing that the measured summit IS the true summit.
It is only when you look at the map more closely (or consult an authoritative source on the location and elevation of the true summit of that mountain peak) that you realize that the measured summit is NOT the true summit. The [nearby] unmeasured summit is undeniably higher in elevation (thanks to the higher contour line) and is the true summit. Another way that you will stumble upon Case #3 is when you consult a respected source for peak information and are puzzled as to how they arrived at an elevation for the peak that doesn’t coincide with the measured elevation.
For example, let’s say we have a peak that has a measured summit of 9,995 feet. But your favorite source for peak information lists the peak’s elevation at 10,020 feet. What’s going on here? You examine your source’s map showing the true summit and it turns out to be an unmeasured area above a contour line. In this case, that contour line is at 10,000 feet. The true summit in this case is between 10,000 feet and 10,039 feet (assuming a 40-foot contour interval). Typically, the respected source will use an interpolated estimated of 10,020 feet. 10,020 feet beats 9,995 feet every time. Even if we assume that the unmeasured summit is only 10,000 feet, it still wins and is correctly awarded the honor of being the true summit for this mountain peak. The measured summit of 9,995 feet sits above a [lower] contour line at 9,960 feet.
Here is an Idaho illustration of Case #3. Mores Mountain has an elevation of 7,260 feet and yet the nearby measured summit is 7,237 feet. The higher summit is to the west of Point 7237, but a quick look at the map might fool you into thinking that the elevation of Mores Mountain is 7,237 feet. Page 144 of the book incorrectly shows the elevation of Mores Mountain as 7,237 feet. The true summit is just west of Point 7237 and has a higher contour line than Point 7237. The true summit is measured at 7240+ feet or an interpolated elevation of 7,260 feet.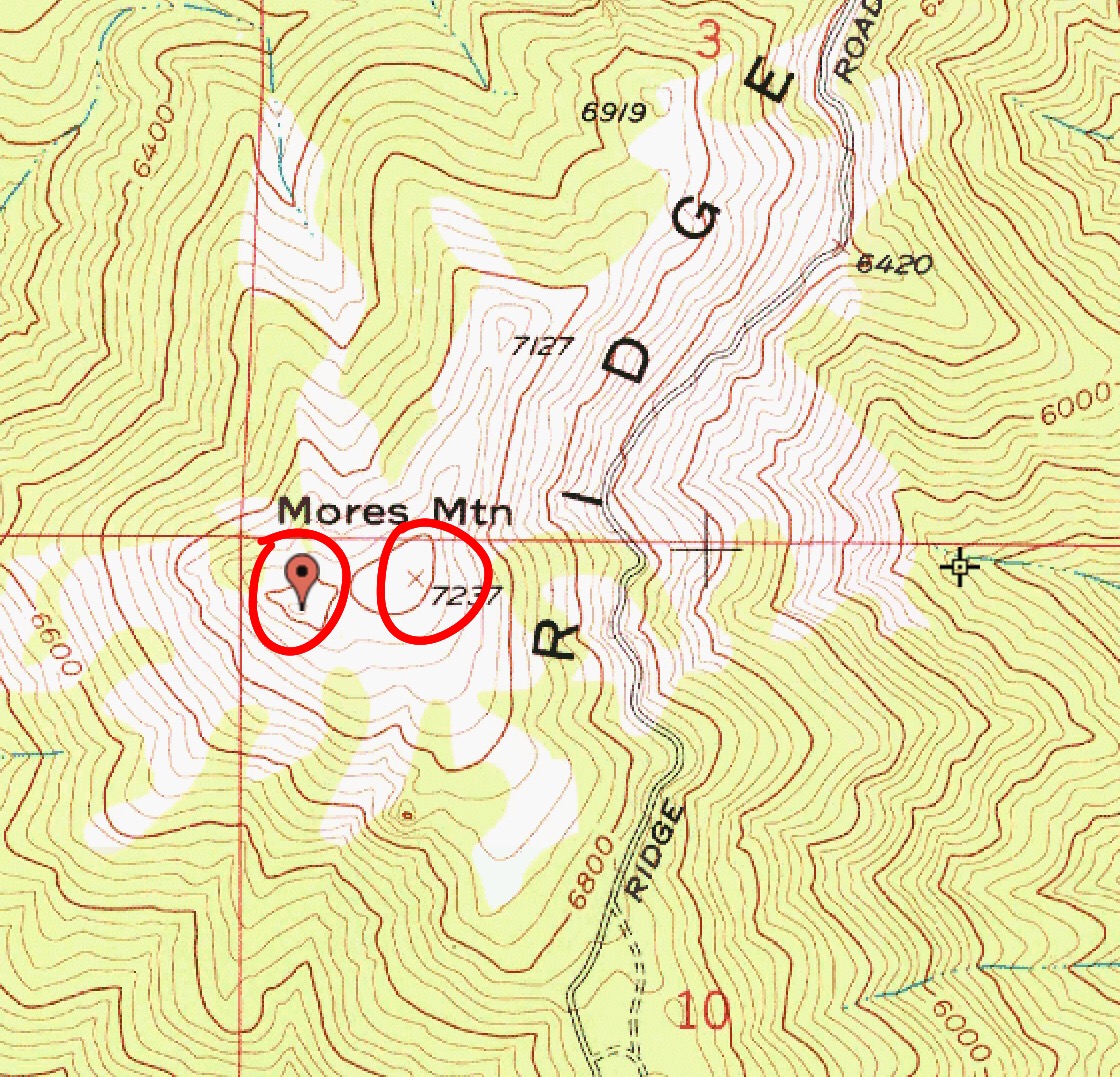
Be VERY CAREFUL when consulting your map(s) to not make the mistake of bagging the [lower] measured false summit. It is remarkably easy to do because the difference between the measured summit elevation and the “highest” contour line might be slim. And if the two points are separated by enough distance, your visual inspection (if you even do one) might just deceive you. This is a case where a respected authority on determining true summits and true elevations is INVALUABLE. I’m not going to name names, but there is one source in particular that is astonishingly good at determining the true summits of thousands of Idaho’s mountains. It’s really amazing.
CASE #4
This is the case where a mountain has two (or more) unmeasured summits of equal height. An unmeasured summit is one that lacks a specific elevation. It is considered the true summit if it is located above the highest contour line for that mountain. But, in Case #4, we have two (or more) possible true summits since we have two (or more) independent, “highest” contour lines of equal height. In this case, we simply don’t know which one is highest. You must stand on each potential summit and make your own determination—visually or, preferably, with the assistance of a GPS or Altimeter reading. Simply assuming that the “highest” contour line with the greatest land area above the contour line is the true summit is a logical, but not sufficient, assessment.
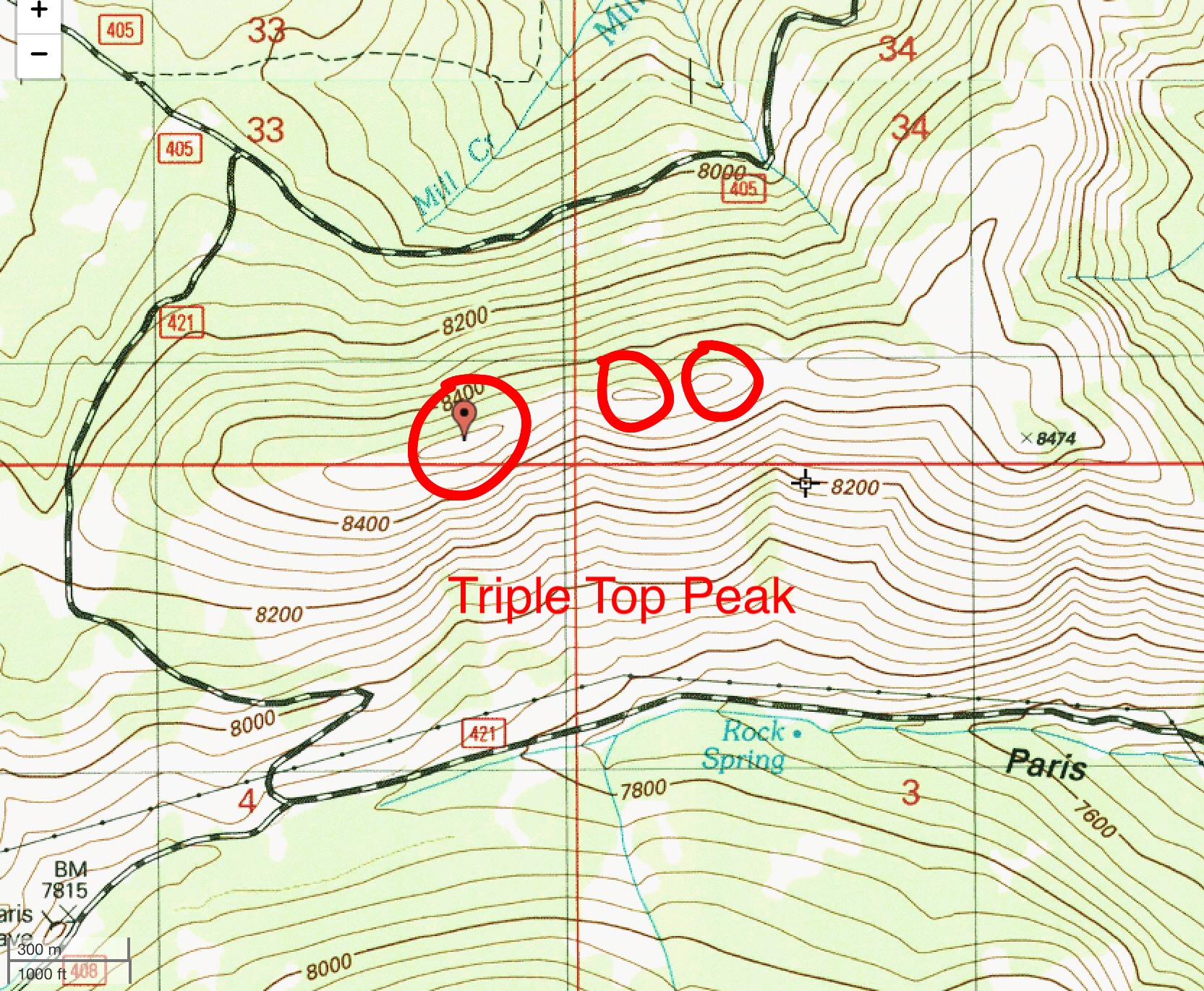
The closer the potential summits, the easier it is to make a subjective assessment. The farther apart the potential summits (and/or the larger the number of potential summits), the more difficult it is to make such an assessment. Tom Lopez made such an assessment on Idaho’s Triple Peak. I made such assessments on both Triple Top Peak and North Sister. In the case of Triple Peak, the contour line with the largest land area above the “highest” contour line is the true summit. However, in the case of Triple Top Peak, the contour line with the largest land mass above the contour line is NOT the true summit. In the case of North Sister (a peak with four potential summits), it was a tie between the third and fourth summits, both of which have similar land area above the “highest” contour line.
As you can see, determining the true summit can be a tricky endeavor. The best advice is to stand atop all of the potential summits, if possible, just to be sure. If the potential summits are close to each other and you can make a visual determination then a visit to each high point seems unnecessary. A small plastic hand level is an essential tool when the highest point is in question. [The following link discusses the use of a hand level in detail: Tips & Techniques for County Highpointing with Hand Levels]
CASE #5
This is the case where a mountain has a measured summit and two (or more) unmeasured summits and all of the aforementioned summits share the same, albeit independent, “highest” contour line. This case raises the most complicated and contentious debate. And, unfortunately, it occurs more often than you would think. In Idaho, illustrations include Kinport Peak and Oxford Peak. The easiest way (and the traditional way) of handling these cases is to simply go with the measured summit and ignore the unmeasured summit(s).
Problems arise when you give the unmeasured summit an exact altitude (typically an interpolation between the “highest” contour line and the next higher contour line). An interpolation is simply the mid-point between the “highest” contour line and the next higher contour line. Contour intervals are typically 40 feet but are sometimes 20 feet (with low elevation peaks) and can be measured in meters as well (typically 20 meters, but sometimes 10 meters). An interpolation is simply an estimate. It is not an exact measurement.
Let’s say that we have a peak with a measured summit of 10,415 feet. The highest contour line for this measured summit is 10,400 feet. We also have an unmeasured summit that shares the same, but independent, contour line at 10,400 feet. Tradition says the true summit is located at the measured summit of 10,415 feet. However, some will assign the unmeasured summit an altitude of 10,420 feet (an interpolation based on a 40-foot contour interval). Comparing the 10,420 altitude to the 10,415 altitude, the unmeasured summit wins and is consecrated as the true summit.
But all we know about the unmeasured summit is that it is somewhere in the 10,400 to 10,439-foot range. We simply don’t know its exact elevation. Is it higher or lower than the 10,415-foot measured summit? We just don’t know. We can, however, do a visual inspection of our own, preferably backed up by a GPS or Altimeter measurement of each summit. From that inspection, we can then subjectively determine the true summit. When you mix interpolations (estimates) with actual measurements, the actual measured summit is thrown by the wayside about half of the time. The other half of the time, the measured summit wins. It’s really a crap-shoot. It’s better to either accept the measured summit as the high point (tradition) or to do a subjective, ON SITE assessment.
CASE #6
This is the case where a mountain has a measured summit but has a higher, unmeasured point that shares the SAME, NON-INDEPENDENT, “highest” contour line. In Idaho, such is the case with Black Peak/Black BM (in the Black Pine Mountains) and Wet Peak (in the Lost River Range). In each of these instances, the true summit is not the USGS benchmark (the measured summit) but is a higher point about 100-150 horizontal feet away. The higher point measures at 10 vertical feet higher than the BM in both of these cases.
Tradition dictates to ignore the unmeasured summit and go with the measured summit. Visual, ON SITE inspection may very well warrant a subjective assessment that the nearby unmeasured summit is somewhat higher. Indeed, on Page 351 of Idaho A Climbing Guide, Black Peak is assigned an elevation of 9,395 feet, 10 feet higher than Black BM (9,385 feet) because of observations of climbers who have done their own ON SITE inspection. I concur with that subjective assessment as I did both a visual and altimeter-based assessment of the two humps. My Altimeter determined Black Peak to be 10 feet higher than the nearby Black BM location (the altimeter measures altitude in 5-foot increments).
Once again, your safest bet as a mountain climber/peak-bagger is to stand atop both the measured summit and the unmeasured summit, JUST TO BE SURE. In Case #6, they are likely to be located fairly close to each other, making for an easy assessment. It is a subjective assessment, however. Sources considered to be reliable/authoritative still rely on the measured summit’s altitude, AS THEY SHOULD.
Case #7
This is the case where there is uncertainty about the location of a summit because of an inconsistency in the USGS topo map measurements. Let’s look at Badger Mountain in the South Hills of Idaho: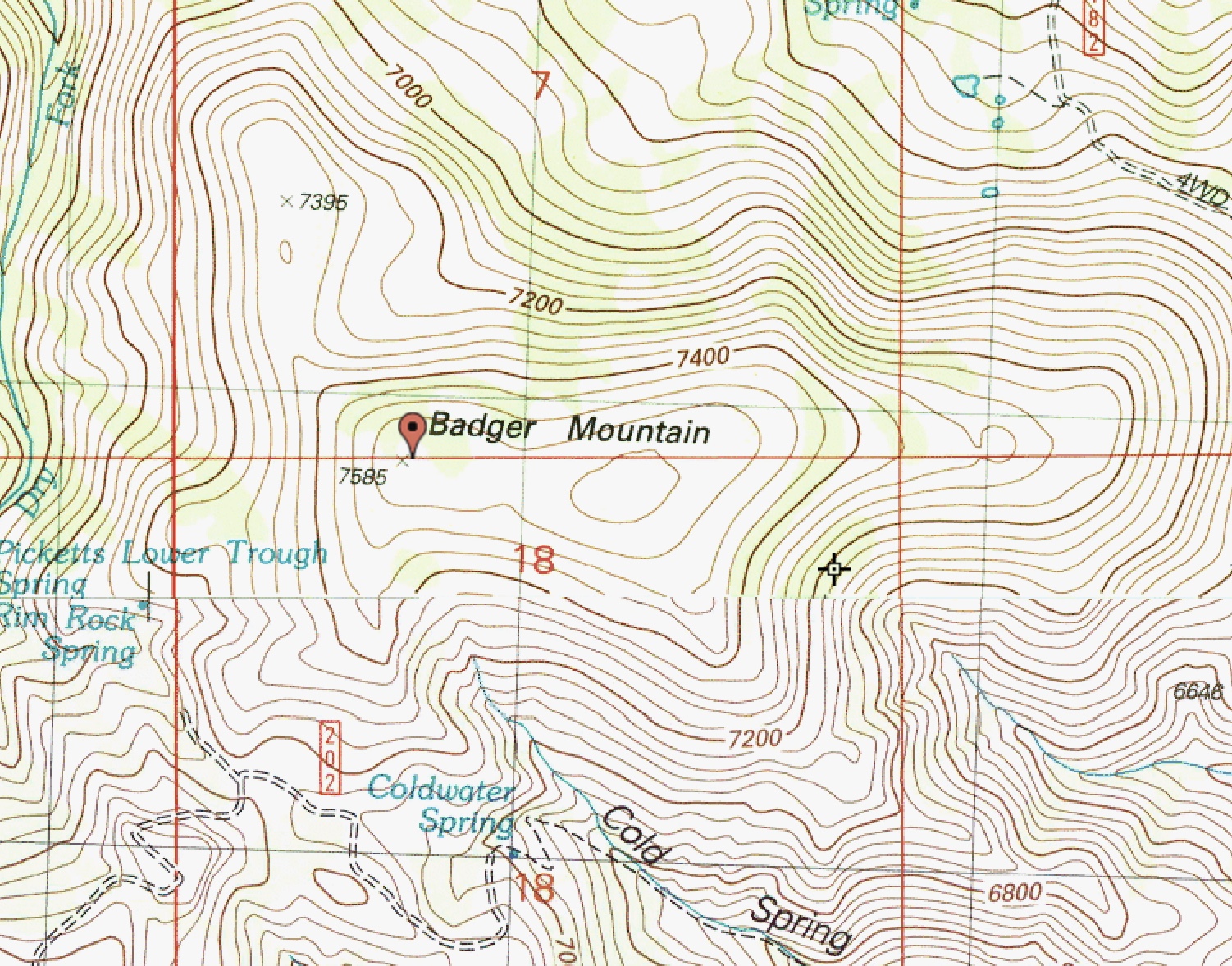
The measured elevation for Badger Mountain is 7,585 feet. The summit is located at the western end of a wide summit plateau. However, the eastern end of the summit area is on a higher contour line (7,560 feet) than the western end (7,520 feet). How can this be? Did the USGS mapmakers intend to place the measured point at the eastern end, above the 7,560-foot contour line? Or did they forget to include a 7,560-foot contour line at the western end? Or is the 7,585-foot figure a mis-measurement?
Where is the actual high point for Badger Mountain? Based on the contour lines, the western end is lower than the eastern end and can’t possibly have the summit high point there. The eastern end has a higher contour line but a lower interpolated elevation (7,580 feet) than the specific point measurement at the western end (7,585 feet). This is all very confusing thanks to inconsistent map representations on the USGS topo map. I stood on the eastern end of Badger Mountain and, as the contour lines indicate, the high point is there. It is visually obvious and there is a summit cairn there as well. In cases like this, you must investigate the summit area for yourself and make your own determination of the location of the high point, ignoring the USGS topo map’s inconsistencies.
What is the true elevation of a summit and how is it determined?
There are two types of true elevations: actual/measured ones and estimated/unmeasured ones. We will discuss each in turn.
Actual/measured summits
In the process of mapping the Western United States, many mountains were measured by the intrepid surveyors working as part of a U.S. Government-funded project. In more recent times, the United States Geological Survey (USGS) has placed specific altitudes on many mountain peaks as well as USGS benchmarks. Periodically, these altitude assessments are updated, as can be seen with a comparison of an [older] 15-minute USGS topo map to a [more recent] 7.5-minute USGS topo map. Tradition is to ascribe the most recent altitude measurement to be the correct one. If an altitude is no longer given on the latest 7.5-minute map, then the [older] 15-minute map assessment is used. In addition, some sources use North America Vertical Datum of 1988 (NAVD88) measurements as a supplement to the [older] USGS topo map measurements.
Regrettably, there are inconsistencies found on USGS maps, data sheets/maps and BGN pages. Here are two examples:
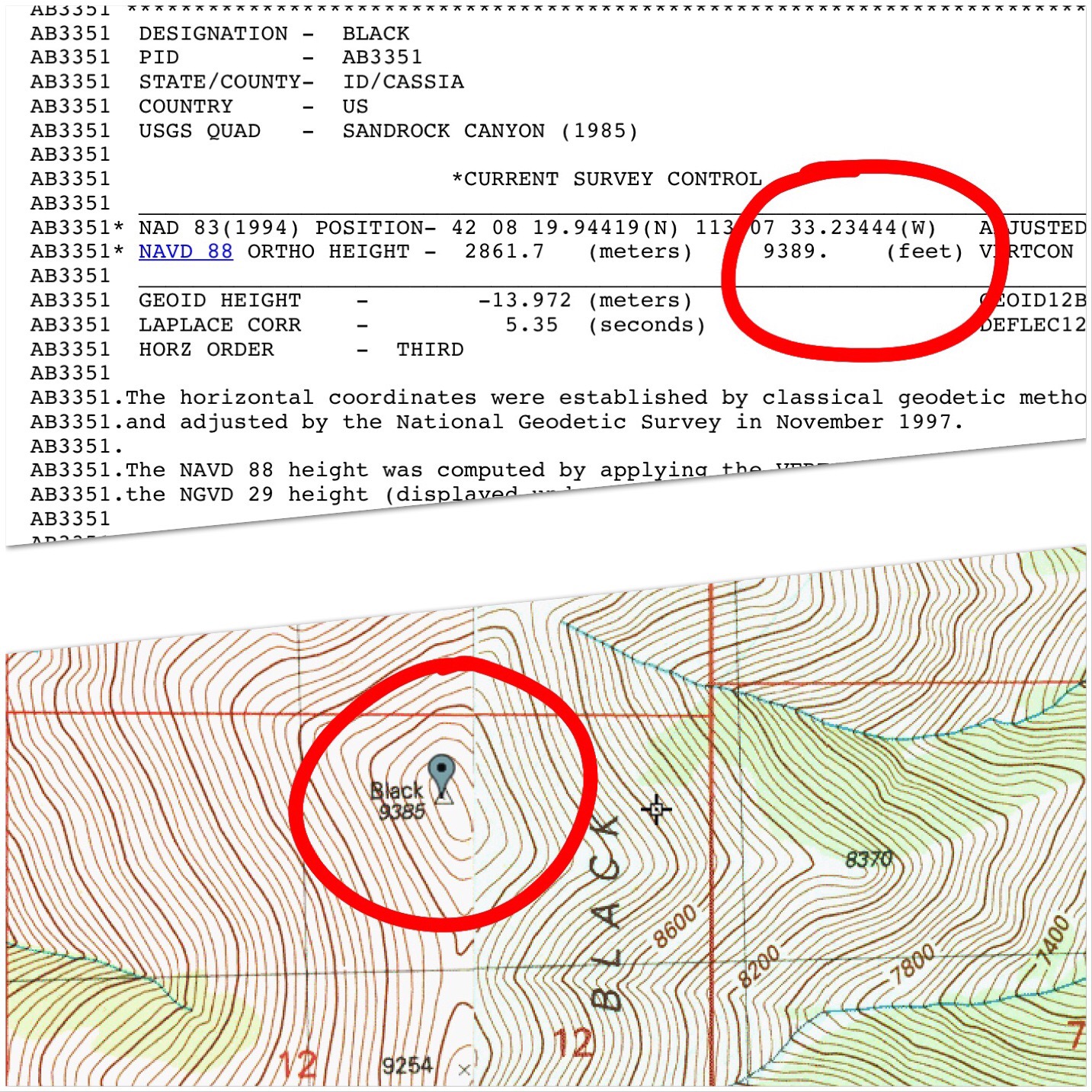
This graphic shows the discrepancy between a USGS map and the underlying data sheet for the Black Benchmark in Idaho’s Black Pine Mountains..

This graphic shows discrepancy between a USGS map and the associated Board of Geographic Names page for Black Pine Peak in the Black Pine Mountains..
In most cases, minor changes (or inconsistencies) in measured altitudes are not terribly important. It can become an issue, however, when comparing two summits of similar height (e.g., Black Pine Peak versus Black Peak/BM) where one peak is a ranked summit and the other is an unranked summit. But, thankfully, that situation is not common. Given the GPS technology that we now have (and perhaps more accurate surveying equipment for ON THE GROUND work), we will probably see some adjustments to specific altitude measurements in the future. And, generally speaking, it’s not a big deal.
Estimated/unmeasured summits
It’s really astonishing how many mountain points and peaks have specific altitude measurements. However, many of the more obscure Idaho peaks lack a specific altitude figure. In these cases, sources rely on the highest contour line as the starting point to make an assessment of a specific altitude for a mountain peak. Typically, an interpolation is used as the specific measure of a peak’s altitude. For example, a peak with a “highest” contour line of 10,400 feet is assigned an altitude of 10,420 feet (assuming a 40-foot contour interval). And, with nothing else to rely on but a topo map with contour lines, such an interpolation is a reasonable estimate. It’s probably more logical than any other estimate. And it’s better than using an ill-defined figure like “10,000+ feet.”
Problems arise when you have a mountain with multiple potential summits (Case #5), one of which is a measured summit. Tradition says to use the measured summit’s altitude and ignore the unmeasured summits entirely. Sources considered to be reliable/authoritative either go with tradition or use the higher of the interpolation and the measured altitude. Others rely on climbers’ ON SITE evaluations.
Given the rather arbitrary nature of comparing interpolations/estimates to actual measured altitudes, I side with tradition on this one. But an ON SITE inspection is not a bad thing. I do it all the time. If you are a purist mountain climber/peak-bagger as I am, you simply must stand on all of the potential high points and make your own determination, if for no other reason than you wish to honestly say that that you stood on the highest point. In cases where a nearby summit is visually [and obviously] lower in altitude, I see no need to stand on the lower summit(s).
That being said, when I stood on the [higher] unmeasured south summit of Kinport Peak and could clearly see that the measured [and accepted] north summit is lower in elevation, I still dropped to a saddle and climbed that northern summit JUST TO BE SURE. And my Altimeter concurred, giving it a 20-foot lower altitude than the [unmeasured, unrecognized] south summit. And I accept the altitude for Kinport Peak as 7,222 feet, even though I know that the actual summit of Kinport Peak is closer to 7,240 feet. Until a recognized, authoritative entity (like the USGS) measures the south summit and confirms my visual (and altimeter-based) assessment, I cannot override the 7,222-foot figure.
Mis-measured summits
This is perhaps the most perplexing case of all and the most difficult to resolve. What is the correct elevation of a mountain peak with a measured altitude that is inconsistent with the USGS map contour lines? Let’s look at Ibex Peak as an illustration. Ibex Peak is an iconic summit located in the South Hills of Idaho. Here is what the USGS topo map shows: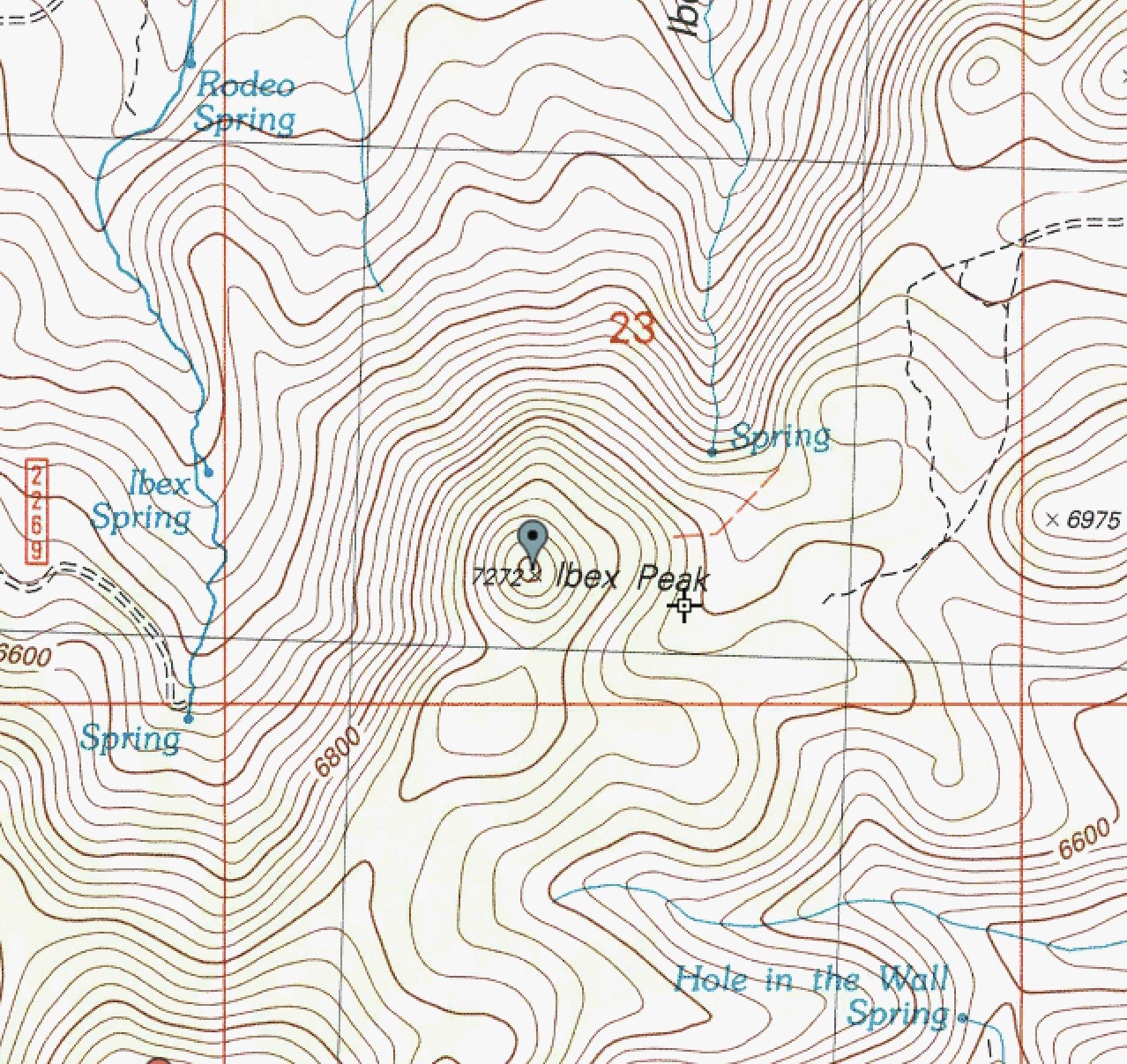
The measured elevation is 7,272 feet and the summit area is pretty small. However, it is impossible for the elevation to be 7,272 feet since the highest contour line is 7,200 feet. Based on the contour lines, the interpolated elevation is 7,220 feet and the maximum elevation is 7,239 feet. Did the USGS mapmakers mis-measure the point elevation (7,272 feet) or fail to include the 7,240-foot contour line? Who knows? The standard convention in this case is to go with the measured elevation of 7,272 feet and ignore the missing contour line(s).
Summary and Conclusions
We can’t always rely on measured estimates of a mountain’s height. Nor can we always be sure that the measured point is the highest point. But neither should we blindly accept interpolations as surrogates for the real thing. We can’t always rely on subjective determinations of where the highest point is (e.g., the contour line with the greatest surface area above it). Sometimes that methodology is correct, sometimes it isn’t.
The best way to deal with all of the possible inaccuracies and estimates is to stand atop every one of the potential high points on a mountain, JUST TO BE SURE. It’s really that simple.
The two most popular websites for climbers are peakbagger.com and ListsofJohn.com. The methodology each of these websites for determining a peak’s elevation is set out below: